【導讀】最近有不少考生問到2023浙江專升本數(shù)學考試大綱出來了嗎?那么就這個問題，下面帶來相關資料，一起參考看看吧。

　　點擊查看：2022年浙江專升本各院校錄取通知書已寄出!(更新中)

　　點擊查看：浙江省2022年專升本各院校錄取通知書發(fā)放時間!

　　點擊進入：2023年浙江專升本報名報考指導入口

　　關注【浙江專升本之家】公眾號，回復【真題】即可獲取最新考試真題。還可以免費領取相關升本課程資料哦!

　　2023浙江專升本數(shù)學考試大綱出來了嗎?

　　目前考試院暫未公布新的考試大綱，因此考生們可以先參考往年的考綱復習。一般來說每年的考綱變動都不是很大。

　　考試要求

　　考生應按本大綱的要求，掌握“高等數(shù)學”中函數(shù)、極限和連續(xù)、一元函數(shù)微分學、一元函數(shù)積分學、無窮級數(shù)、常微分方程、向量代數(shù)與空間解析幾何的基本概念、基本理論和基本方法。考生應注意各部分知識的結構及知識的聯(lián)系;具有一定的抽象思維能力、邏輯推理能力、運算能力和空間想象能力;能運用基本概念、基本理論和基本方法進行推理、證明和計算;能運用所學知識分析并解決一些簡單的實際問題。

　　考試內(nèi)容

　　一、函數(shù)、極限和連續(xù)

　　(一)函數(shù)

　　1.理解函數(shù)的概念，會求函數(shù)的定義域、表達式及函數(shù)值，會作出一些簡單的分段函數(shù)圖像。

　　2.掌握函數(shù)的單調(diào)性、奇偶性、有界性和周期性。

　　3.理解函數(shù)y =?(x)與其反函數(shù)y =?-1(x)之間的關系(定義域、值域、圖像)，會求單調(diào)函數(shù)的反函數(shù)。

　　4.掌握函數(shù)的四則運算與復合運算; 掌握復合函數(shù)的復合過程。

　　5.掌握基本初等函數(shù)的性質(zhì)及其圖像。

　　6.理解初等函數(shù)的概念。

　　7.會建立一些簡單實際問題的函數(shù)關系式。

　　(二)極限

　　1.理解極限的概念(只要求極限的描述性定義)，能根據(jù)極限概念描述函數(shù)的變化趨勢。理解函數(shù)在一點處極限存在的充分必要條件，會求函數(shù)在一點處的左極限與右極限。

　　2.理解極限的唯一性、有界性和保號性，掌握極限的四則運算法則。

　　3.理解無窮小量、無窮大量的概念，掌握無窮小量的性質(zhì)，無窮小量與無窮大量的關系。會比較無窮小量的階(高階、低階、同階和等價)。會運用等價無窮小量替換求極限。

　　4.理解極限存在的兩個收斂準則(夾逼準則與單調(diào)有界準則)，掌握兩個重要極限：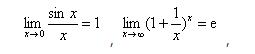

　　并能用這兩個重要極限求函數(shù)的極限。

　　(三)連續(xù)

　　1.理解函數(shù)在一點處連續(xù)的概念，函數(shù)在一點處連續(xù)與函數(shù)在該點處極限存在的關系。會判斷分段函數(shù)在分段點的連續(xù)性。

　　2.理解函數(shù)在一點處間斷的概念，會求函數(shù)的間斷點，并會判斷間斷點的類型。

　　3.理解“一切初等函數(shù)在其定義區(qū)間上都是連續(xù)的”，并會利用初等函數(shù)的連續(xù)性求函數(shù)的極限。

　　4.掌握閉區(qū)間上連續(xù)函數(shù)的性質(zhì)：最值定理(有界性定理)，介值定理(零點存在定理)。會運用介值定理推證一些簡單命題。

　　二、一元函數(shù)微分學

　　(一)導數(shù)與微分

　　1.理解導數(shù)的概念及其幾何意義，了解左導數(shù)與右導數(shù)的定義，理解函數(shù)的可導性與連續(xù)性的關系，會用定義求函數(shù)在一點處的導數(shù)。

　　2.會求曲線上一點處的切線方程與法線方程。

　　3.熟記導數(shù)的基本公式，會運用函數(shù)的四則運算求導法則，復合函數(shù)求導法則和反函數(shù)求導法則求導數(shù)。會求分段函數(shù)的導數(shù)。

　　4.會求隱函數(shù)的導數(shù)。掌握對數(shù)求導法與參數(shù)方程求導法。

　　5.理解高階導數(shù)的概念，會求一些簡單的函數(shù)的n階導數(shù)。

　　6.理解函數(shù)微分的概念，掌握微分運算法則與一階微分形式不變性，理解可微與可導的關系，會求函數(shù)的一階微分。

　　(二)中值定理及導數(shù)的應用

1. 理解羅爾(Rolle)中值定理、拉格朗日(Lagrange)中值定理及它們的幾何意義，理解柯西(Cauchy)中值定理、泰勒(Taylor)中值定理。會用羅爾中值定理證明方程根的存在性。會用拉格朗日中值定理證明一些簡單的不等式。

   
   

　　3.會利用導數(shù)判定函數(shù)的單調(diào)性，會求函數(shù)的單調(diào)區(qū)間，會利用函數(shù)的單調(diào)性證明一些簡單的不等式。

　　4.理解函數(shù)極值的概念，會求函數(shù)的極值和最值，會解決一些簡單的應用問題。

　　5.會判定曲線的凹凸性，會求曲線的拐點。

　　6.會求曲線的漸近線(水平漸近線、垂直漸近線和斜漸近線)。

　　7.會描繪一些簡單的函數(shù)的圖形。

　　三、一元函數(shù)積分學

　　(一)不定積分

　　1.理解原函數(shù)與不定積分的概念及其關系，理解原函數(shù)存在定理，掌握不定積分的性質(zhì)。

　　2.熟記基本不定積分公式。

　　3.掌握不定積分的第一類換元法(“湊”微分法)，第二類換元法(限于三角換元與一些簡單的根式換元)。

　　4.掌握不定積分的分部積分法。

　　5.會求一些簡單的有理函數(shù)的不定積分。

　　(二)定積分

　　1.理解定積分的概念與幾何意義, 掌握定積分的基本性質(zhì)。

　　2.理解變限積分函數(shù)的概念，掌握變限積分函數(shù)求導的方法。

　　3.掌握牛頓—萊布尼茨(Newton—Leibniz)公式。

　　4.掌握定積分的換元積分法與分部積分法。

　　5.理解無窮區(qū)間上有界函數(shù)的廣義積分與有限區(qū)間上無界函數(shù)的瑕積分的概念，掌握其計算方法。

　　6.會用定積分計算平面圖形的面積以及平面圖形繞坐標軸旋轉(zhuǎn)一周所得的旋轉(zhuǎn)體的體積。

　　四、無窮級數(shù)

　　(一)數(shù)項級數(shù)

1. 理解級數(shù)收斂、級數(shù)發(fā)散的概念和級數(shù)的基本性質(zhì)，掌握級數(shù)收斂的必要條件。

   
   

　　3.理解任意項級數(shù)絕對收斂與條件收斂的概念。會用萊布尼茨(Leibnitz) 判別法判別交錯級數(shù)的斂散性。

　　(二)冪級數(shù)

　　1.理解冪級數(shù)、冪級數(shù)收斂及和函數(shù)的概念。會求冪級數(shù)的收斂半徑與收斂區(qū)間。

　　2.掌握冪級數(shù)和、差、積的運算。

　　3.掌握冪級數(shù)在其收斂區(qū)間內(nèi)的基本性質(zhì)：和函數(shù)是連續(xù)的、和函數(shù)可逐項求導及和函數(shù)可逐項積分。

　　五、常微分方程

　　(一)一階常微分方程

　　1.理解常微分方程的概念，理解常微分方程的階、解、通解、初始條件和特解的概念。

　　2.掌握可分離變量微分方程與齊次方程的解法。

　　3.會求解一階線性微分方程。

　　(二)二階常系數(shù)線性微分方程

　　1.理解二階常系數(shù)線性微分方程解的結構。

　　2.會求解二階常系數(shù)齊次線性微分方程。

　　六、向量代數(shù)與空間解析幾何

　　(一)向量代數(shù)

　　1.理解向量的概念，掌握向量的表示法，會求向量的模、非零向量的方向余弦和非零向量在軸上的投影。

　　2.掌握向量的線性運算(加法運算與數(shù)量乘法運算)，會求向量的數(shù)量積與向量積。

　　3.會求兩個非零向量的夾角，掌握兩個非零向量平行、垂直的充分必要條件。

　　(二)平面與直線

　　1.會求平面的點法式方程與一般式方程。會判定兩個平面的位置關系。

　　2.會求點到平面的距離。

　　3.會求直線的點向式方程、一般式方程和參數(shù)式方程。會判定兩條直線的位置關系。

　　4.會求點到直線的距離，兩條異面直線之間的距離。

　　5.會判定直線與平面的位置關系。

　　試卷結構

　　試卷總分：150分

　　考試時間：150分鐘

　　試卷內(nèi)容比例：

　　函數(shù)、極限和連續(xù) 約20%

　　一元函數(shù)微分學 約30%

　　一元函數(shù)積分學 約30%

　　無窮級數(shù)、常微分方程　　　　　　　　　　　　　 約15%

　　向量代數(shù)與空間解析幾何　　　　　　　　　　　　 約5%

　　試卷題型分值分布：

　　選擇題共 5題，每小題 4 分，總分20分;

　　填空題共10題，每小題 4 分，總分40分;

　　計算題共 8題，　　　　　　 總分60分;

　　綜合題共 3題，每小題10分，總分30分。

　　以上就是關于“2023浙江專升本數(shù)學考試大綱出來了嗎?”的全部內(nèi)容，若考生還想了解更多關于浙江專升本考試的相關資訊，如浙江統(tǒng)招專升本考試政策、考試大綱、常見問題、統(tǒng)招考試、成績查詢、錄取分數(shù)線等，可加入【浙江專升本考生交流群】，一起升本上岸，有問題也可【在線咨詢】老師為你解答哦!